
From Heavy Hitters to Lazy Decay: Learning to Forget at Scale
Originally published on Medium: From Heavy Hitters to Lazy Decay: Learning to Forget at Scale
I’d been reading about how large systems handle hot keys, the tiny fraction of IDs or cache entries that suddenly get hammered with traffic.
Everyone talks about detecting and caching them automatically, in real time.
At first, I just wanted to understand how you’d even detect what’s hot right now. I didn’t plan to build anything. I was chasing an idea.
I started with the obvious tools: a Count-Min Sketch (CMS) to estimate frequencies, and maybe a small top-K heap to keep the heaviest hitters on record.
It all made sense… until I realised something fundamental: they don’t forget.
You need a way to know what’s hot now. With this design, once a key becomes hot, it stays hot forever because its old counts never fade. Think of it as YouTube still thinking Gangnam Style is trending or that meme you posted which went viral is still lurking around in Reddit’s cache.
I needed a rolling window view, something like “last 5 minutes.”
My first thought was to slice time into buckets. I thought I can keep 12 CMS instances, one per 5-second slice, and always sum the last twelve to represent the most recent minute.
That worked in theory, but it felt clumsy. The memory footprint multiplied, merging got messy, and the data jumped discontinuously whenever a bucket rotated out.
I wanted a smoother sense of time. A system that continuously forgets.
That’s how I stumbled onto exponential decay.
Exponential decay has a kind of mathematical grace to it. Each count just shrinks by a factor as time passes that guarantees it to be halved in predefined time and fadeout over time.
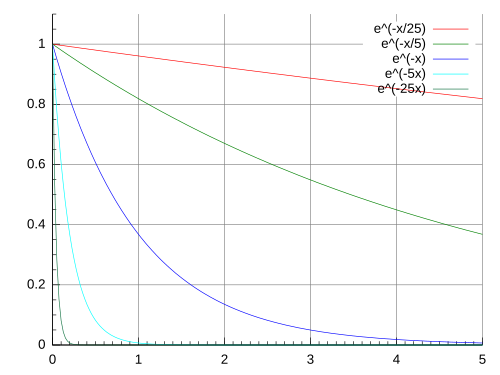
Of course this wasn’t the answer but I felt I was getting closer. The problem this time is closer to heart as a I spent some time in another life thinking about algorithmic complexities. This algorithm requires O(N) work every tick. If N is in the millions, I can build a very elegant CPU heater.
At that point, I asked ChatGPT about it. It started talking about some kind of wizardry I hadn’t seen before. Maybe it was my rusty CS fundamentals, but it took me a bit to really grasp it. That’s what triggered me to write about it here.
You don’t have to decay every counter. Just keep a global decay factor.
At first that sounded impossible. How could a single number replace a million multiplications? Then I worked it out, and it suddenly made perfect sense.
All exponential decay means is multiplying by the same factor over time, and as I learnt 20+ years ago, multiplication is commutative. You can apply it now, later, or never; the math is identical.
So instead of touching every counter, you maintain one variable:
G = 1.0 # global decay factor
last_decay = now()
λ = 1 / τ # decay rate
Each time time moves forward, update it:
Δt = now() - last_decay
G *= exp(-λ * Δt)
last_decay = now()
Then, when adding a new event, scale it by the inverse of that global decay:
cms[row][hash_i(key)] += 1.0 / G
and when reading, multiply the estimate by G:
est = min(cms[row][hash_i(key)] for row in cms_rows)
return est * G
Mathematically, the scaling cancels → (1 / G) × G = 1
Every new event counts exactly as one hit now. Everything that happened in the past quietly fades as G shrinks.
No loops. No background sweeps. The whole structure forgets continuously.
At that moment, the idea clicked completely. All the counters live in a decayed coordinate system. You’re not storing real counts, you’re storing counts divided by G. As time moves forward, that coordinate system compresses. When you multiply by G again on read, you get the current reality. Elegant, right?
What fascinates me now is how general the pattern is. It’s one of those ideas that’s both mathematical and deeply practical yet simple. You can forget continuously without ever looping over your past.